Vondrak¶
A Python implementation of Vondrák’s long term precession model and Fortran code.
Introduction¶
The earth, like a wobbling top, has an axial precession which complete’s one complete cycle in approximately 26,000 years. Astronomers often choose a favorite epoch, such as J2000, to express the coordinates of astronomical bodies in celestial coordinates. To convert between orientations, one must use a rotational matrix. This project implements the Vondrák long term precession model to create such a rotational precession matrix. This is relatively accurate for hundreds of thousands of years.
All credit for this precession model goes to Jan Vondrák and his colleagues.
Implementation¶
A rotation matrix allows us to perform a rotation in Euclidean space. The rotation matrix obtained by using the Vondrák ltp model allows us to convert between the celestial orientation of J2000 and another epoch year.
A new position, or orientation, whether for the past or future, can be obtained by computing a rotation matrix for the epoch date of choice. This rotation matrix is then applied to the coordinates of the standard epoch to precess the position. p₁ = P·p₀, where P is the precession matrix and p₀ is the original position. P is computed for every epoch date that one wishes to orient to.
We now have the new celestial coordinates p₁ expressed in the new reference epoch. The date is specified in the original computation of position with respect to the standard epoch and then maintained when the rotation matrix is applied.
Additionally, we can convert the coordinates of another epoch to the standard epoch by inverting the precession matrix. We transpose this like so
References¶
- Some New Thoughts About Long-Term Precession (2010)
- New Long-Term Expressions for Precession (2011)
- New precession expressions, valid for long time intervals (2011)
- New precession expressions, valid for long time intervals (Corrigendum) (2012)
The documentation is available through the links in the Table of Contents below.
You can also visit:
- Official Python Package Index entry
- GitHub project page
- GitHub issue tracker
Table of Contents¶
Installation¶
There is only one dependency for Vondrak, NumPy. You can install with pip install numpy. You can install Vondrak as well with the standard Python package tool
pip install vondrak
If you have any problems with installation, or would like to suggest an improvement, simply create an issue on the project’s Github page:
Cheers!
Examples¶
Some basic usage of the Vondrak module.
Periodicity¶
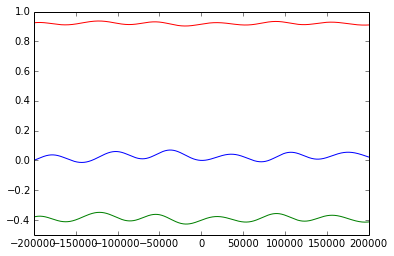
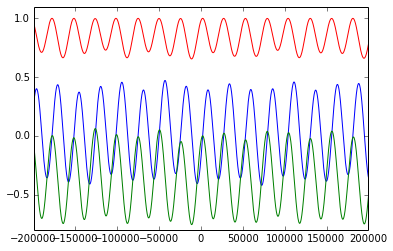
This first example, shows the periodicity of ecliptic and equatorial components of the matrix over 400000 years.
%pylab inline
Populating the interactive namespace from numpy and matplotlib
import vondrak as v
ecl_p_matrix_list = []
equ_p_matrix_list = []
year = arange(-200001.0, 200000.0, 100)
for y in year:
p_ecl = v.ltp_PECL(y)
p_equ = v.ltp_PEQU(y)
ecl_p_matrix_list.append(p_ecl)
equ_p_matrix_list.append(p_equ)
axis([-200000,200000,-.5,1])
plot(year, ecl_p_matrix_list)
show()
axis([-200000,200000,-.8,1.1])
plot(year, equ_p_matrix_list)
show()
Implementation¶
We then will show how to take an initial position (for Polaris) at J2000, and use the rotation matrix to find the new celestial coordinates computed for a new epoch.
The new positions (future or past of J2000) are optained by multiplying the coordinates of the standard epoch by the precession matrix. p₁ = P·p₀, where P is the below precession matrix and p₀ is the original position. The precession matrix is unitless.
P is recomputed for every epoch date.
We now have the new celestial coordinates p₁ expressed in the new reference epoch. The date is specified in the original computation of position in J2000 and then maintened when the rotation matrix is applied.
Additionally, we can convert the coordinates of another epoch to J2000 by inverting the precession matrix. We transpose this like so
Polaris¶
def position_matrix(ra=None, dec=None, x=None, y=None, z=None):
if(ra == None or dec == None):
ra = 0.0
dec = 0.0
if(x==None or y ==None or z==None):
x = cos(dec) * cos(ra)
y = cos(dec) * sin(ra)
z = sin(dec)
return array([[x], [y], [z]])
def compute_polaris(year):
import ephem
polaris = ephem.star('Polaris')
polaris.compute(str(year),epoch='2000')
ra = polaris.a_ra
dec = polaris.a_dec
return position_matrix(ra=ra,dec=dec)
from ephem import hours as hrs
from ephem import degrees as deg
p0 = compute_polaris(2000)
(ra, dec) = v.ra_dec(p0)
print('RA: {}'.format(hrs(ra)))
print('DEC: {}'.format(deg(dec)))
print('cartesian position of Polaris in the year=2000, epoch=2000:')
x = p0[0][0]
y = p0[1][0]
z = p0[2][0]
print('{}\nthis vector has length {}'.format(
(x,y,z),sqrt(x*x + y*y + z*z)))
RA: 2:31:47.10
DEC: 89:15:51.0
cartesian position of Polaris in the year=2000, epoch=2000:
(0.010127331660770541, 0.007897050033378511, 0.99991753347673784)
this vector has length 1.0
p0 = compute_polaris(2000)
print('The position of Polaris at J2000 is \n{}'.format(p0))
epj = 100000
P = v.ltp_PBMAT(epj) # Precession matrix, GCRS
p1 = compute_polaris(epj)
p1 = v.pdp(P, p1)
print('The new position of Polaris in 100000 years is \n{}'.format(p1))
The position of Polaris at J2000 is
[[ 0.01012733]
[ 0.00789705]
[ 0.99991753]]
The new position of Polaris in 100000 years is
[[ 0.31728427]
[-0.15847663]
[ 0.9349951 ]]
(ra, dec) = v.ra_dec(p0)
print('In hours of right ascension and degrees of declination')
print('The position of Polaris at J2000 is')
print(str(hrs(ra)),str(deg(dec)))
print('The new position of Polaris at 100000 years is')
(ra1, dec1) = v.ra_dec(p1)
print(str(hrs(ra1)),str(deg(dec1)))
In hours of right ascension and degrees of declination
The position of Polaris at J2000 is
('2:31:47.10', '89:15:51.0')
The new position of Polaris at 100000 years is
('-1:46:09.87', '69:13:38.5')
from mpl_toolkits.basemap import Basemap
width = 9000000
bm = Basemap(width=width, height=width, projection='aeqd',
lat_0=70.0, lon_0=280.0)
bm.drawparallels(np.arange(-80,81,10))
bm.drawmeridians(np.arange(-180,180,10))
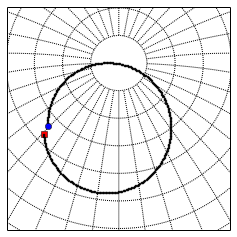
# Position of Polaris at J2000 is p0
years = arange(-13001, 13000, 100)
for year in years:
P = v.ltp_PBMAT(year) # Precession matrix, GCRS
p_1 = compute_polaris(year)
p_1 = v.pdp(P, p1)
(ra1, dec1) = v.ra_dec(p_1)
x, y = bm(degrees(ra1), degrees(dec1))
if(year == years[0]):
bm.plot(x,y, marker='s', color='r')
elif(year == years[-1]):
bm.plot(x,y, marker='o', color='b')
else:
bm.plot(x,y, marker='.', color='black', markersize=4)
print('one cycle of precession is ~26 thousand years')
one cycle of precession is ~26 thousand years
width = 9000000
bm = Basemap(width=width, height=width, projection='aeqd',
lat_0=70.0, lon_0=280.0)
bm.drawparallels(np.arange(-80,81,10))
bm.drawmeridians(np.arange(-180,180,10))
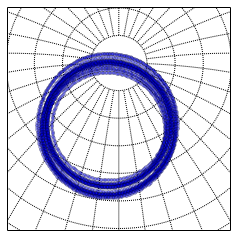
for year in range(-200001, 200000, 100):
P = v.ltp_PBMAT(year) # Precession matrix, GCRS
p_1 = compute_polaris(year)
p_1 = v.pdp(P, p_1)
(ra1, dec1) = v.ra_dec(p_1)
x, y = bm(degrees(ra1), degrees(dec1))
bm.plot(x,y, marker='o', color='blue', alpha=0.3, ms=3)
print('here is 400000 years of Polaris\' precession')
here is 400000 years of Polaris' precession
Vondrak API¶
- vondrak.ltp_PBMAT(jepoch)[source]¶
Long-term precession matrix, including GCRS frame bias.
Given Julian epoch (TT)
Return precession-bias matrix, J2000.0 to date
ltp_PBMAT generates the 3 × 3 rotation matrix P × B, where B is the “frame bias matrix” that expresses the relative orientation of the GCRS and mean J2000.0 reference systems. A simple first-order implementation of the frame bias is used, the departure from rigor being well under 1 μas.
The matrix is in the sense P_date = RPB x P_J2000, where P_J2000 is a vector in the Geocentric Celestial Reference System, and P_date is the vector with respect to the Celestial Intermediate Reference System at that date but with nutation neglected.
A first order bias formulation is used, of sub-microarcsecond accuracy compared with a full 3D rotation.
- vondrak.ltp_PECL(jepoch)[source]¶
Long-term precession of the ecliptic
Given Julian epoch (TT).
Return ecliptic pole unit vector.
ltp_PECL generates the unit vector for the pole of the ecliptic, using the series for Pₐ, Qₐ. The vector is with respect to the J2000.0 mean equator and equinox.
- vondrak.ltp_PEQU(jepoch)[source]¶
Long-term precession of the equator
Given Julian epoch (TT)
Return equator pole unit vector
ltp_PEQU generates the unit vector for the pole of the equator, using the series for Xₐ, Yₐ. The vector is with respect to the J2000.0 mean equator and equinox.
- vondrak.ltp_PMAT(jepoch)[source]¶
Long-term precession matrix
Given Julian epoch (TT)
Return precession matrix, J2000.0 to date
ltp_PMAT generates the 3 × 3 rotation matrix P, constructed using Fabri parameterization (i.e. directly from the unit vectors for the ecliptic and equator poles). The resulting matrix transforms vectors with respect to the mean equator and equinox of epoch 2000.0 into mean place of date.
The matrix is in the sense P_date = RP x P_J2000, where P_J2000 is a vector with respect to the J2000.0 mean equator and equinox and P_date is the same vector with respect to the equator and equinox of epoch EPJ.
- vondrak.pdp(a, b)[source]¶
p-vector inner (=scalar=dot) product.
Given two p-vectors (a and b)
Return a * b
- vondrak.pn(p)[source]¶
Convert a p-vector into modulus and unit vector.
Given p-vector (p)
Return modulus (r), and unit vector (u)